EXERCÍCIO 01 – Exame 2011, 2.ª Fase (código 708)
Determine as projeções da reta de interseção, i, do plano oblíquo ALFA; com o plano de rampa ρ.
Dados:
− o plano ALFA; está definido por uma reta de maior declive, d;
− a reta d contém o ponto P (– 2; 3; 4 );
− as projeções, horizontal e frontal, da reta d fazem, com o eixo x,ângulos de 30º, de abertura para a esquerda, e de 50º, de abertura para a direita, respetivamente;
− os traços horizontal e frontal do plano ρ têm – 5 de afastamento e 7 de cota, respetivamente.

AULA de HOJE - 27 de FEVEREIRO - 10ºA

 10ºA - 8:15 às 10:05

Sumário: Exercícios de Interseções entre Planos. Continuação do estudo de interseções.

EXERCÍCIO 01: 1982, 1.ª Fase, 2.ª Chamada (código 121)
Determine as projeções da reta de interseção dos planos αlfa e β.
Dados:
– o plano α é definido pela reta de maior declive d;
– o traço horizontal da reta d tem 3 de afastamento e as suas projeções, horizontal e frontal, fazem com o eixo x, ângulos de 45º de abertura para a esquerda;
– o plano β é oblíquo aos planos de projeção, interseta o eixo x no ponto N à distância de 6 para a direita da linha de chamada do traço horizontal da reta de maior declive do plano α e os seus traços, horizontal e frontal, fazem com o eixo x, ângulos respetivamente iguais a 45º e 70º de abertura para a esquerda.

EXERCÍCIO 02: 
Desenhe as projeções da reta i de interseção dos planos oblíquos α e θ sabendo que:
·      O plano oblíquo α está definido por uma reta de maior inclinação i que contém o ponto A ( 0; -3; 4 ), e o ponto I do β_2/4 com -2,5cm de abcissa e 2,5cm de cota;
·      O plano θ tem os traços coincidentes e a sua projeção horizontal faz 30⁰ (a.e.) com o eixo X;

·  ·      O plano θ contém o Ponto K da linha X com 3 cm de abcissa

-

                                               

AULA de HOJE - 16 de FEVEREIRO - 11ºA

11ºA - 13:30 às 15:20

SUMÁRIO: Exercícios de consolidação de aprendizagens.

EXERCÍCIO Tipo 01:
Determine a reta de interseção i do plano de topo π com o plano oblíquo α.
Dados:
– o plano de topo π interseta o eixo x no ponto de abcissa 5 e faz, com o plano horizontal de projeção, um diedro (ângulo) de 60º, de abertura para a direita;
– o plano oblíquo α é definido por uma reta de perfil p e pelo ponto C (0; 2; 2);
– a reta de perfil p contém os pontos A (6; 6; 2) e B (6; 2; 6).

EXERCÍCIO Tipo 02:- Verdadeira grandeza de figura
EXERCÍCIO PROFESSOR JOÃO :
- Determine as projeções de um quadrado ABCD existente num plano de rampa PI sabendo que:
O traço frontal do plano PI tem 6 cm de cota;
 - A Abcissa e o Afastamento do vértice A são iguais a zero;
- A diagonal AC mede 11 cm;
- O vértice C tem 3 cm de abcissa e pertence ao Plano Horizontal de Projeção.

EXERCÍCIO Tipo 03: Sombras

bom trabalho

JS

AULA de HOJE - 16 de FEVEREIRO - 10ºB e 10ºA

10ºB e 10ºA - 8:15 às 10:05 e 15:20 às 17:10

Sumário: Exercícios de Interseções entre Planos. Continuação do estudo de interseções.

EXERCÍCIO 01:

Determine as projeções da reta i de interseção dos planos oblíquos Alfa e Beta, sabendo que;

- Os traços horizontal e frontal do plano Alfa fazem, com o eixo X, 40º (a.e.) e 60º (a.d.) respetivamente, e são concorrentes no ponto de abcissa nula;

- O traço frontal do plano Beta é paralelo ao traço horizontal do plano Alfa;

- O plano Beta contém o ponto R (0; 2,5; 2) de uma reta r cujas projeções frontal e horizontal são perpendiculares às projeções frontal e horizontal do plano Alfa.

EXERCÍCIO 02: - 2000, 2.ª Fase (código 109)
Determine a reta de interseção i do plano de topo π com o plano oblíquo α.
Dados:
– o plano de topo π interseta o eixo x no ponto de abcissa 5 e faz, com o plano horizontal de projeção, um diedro (ângulo) de 60º, de abertura para a direita;
– o plano oblíquo α é definido por uma reta de perfil p e pelo ponto C (0; 2; 2);
– a reta de perfil p contém os pontos A (6; 6; 3) e B (6; 3; 6).

EXERCÍCIO 03:

Determine a reta i de interseção de dois planos oblíquos, α e γ, sabendo que:
- O plano α interseta X num ponto com -7 cm de abcissa e os seus traços horizontal e frontal fazem, respetivamente, ângulos de
60º (a.e.) e 35º (a.e.) com o eixo X:
- O plano γ é definido pelos pontos A (0; 4; 6), B (2; 6; 2)
e C (4; 4; 2)

AULA de HOJE - 15 de FEVEREIRO - 11ºA

11ºA - 10:20 às 12:10

SUMÁRIO: Exercícios de consolidação de aprendizagens.
Sombras de cilindros oblíquos.

Vídeo de como se executa sombra de cilindro oblíquo:

EXERCÍCIO Professor João:

Determine as sombras próprias e projetadas de um cilindro oblíquo de bases horizontais, sabendo que:

DADOS:

- O ponto O ( 0; 3,5; 0 ) é o centro da base de menor cota do sólido;

- O cilindro tem 6 cm de altura e o seu eixo faz na projeção horizontal 30º (a.d.)

e na projeção frontal faz 70º (a.d.) com o eixo X:

- A base de menor cota é tangente ao Plano Frontal de Projeção.

AULA de HOJE - 14 de FEVEREIRO - 10ºB

10ºB - 8:15 às 10:05

EXERCÍCIO 01

- Determine a reta i de interseção do planos de rampa 𝞭 e plano passante ψ sabendo que:

O plano passante ψ contém o ponto S ( 0; -5; 5 ).

O plano de rampa 𝞭 contém o ponto P ( -2; 5; -2) e o seu traço frontal tem -5 cm de cota. 

EXERCÍCIO 02 - 2009, 2.ª Fase (código 708)
Determine as projeções da reta de interseção, i, do plano oblíquo π com o plano passante θ .
Dados:
– o plano π interseta o eixo x no ponto com 5 de abcissa;
– os traços horizontal e frontal do plano π fazem, respetivamente,ângulos de 50º e de 30º, ambos de abertura para a direita, com o eixo x;
– o plano θ é definido pelo eixo x e pelo ponto P (0; 3; 6).

EXERCÍCIO 03:

Desenhe as projeções da reta i de interseção do plano passante ω e do plano oblíquo δ sabendo que:

• O plano passante ω contém o ponto A ( 0; -2; 4 );
• O plano oblíquo δ contém os pontos S ( 6; 7; 5 ) e R ( -4; 1; 5 );
• Os traços do plano δ encontram o eixo X num ponto de menos 4 cm de abcissa. 

EXERCÍCIOS de INTERSEÇÕES - aula 10º ano

 10ºB

2003, 1.ª Fase, 1.ª Chamada
EX1: Determine as projeções da reta i de interseção do plano ν com o plano α.
Dados:
– o plano ν é horizontal e contém um ponto A (5; 3; 7);
– o plano a é oblíquo e contém o ponto B (– 5; 2; 3);
– o traço horizontal do plano α cruza o eixo x no ponto de abcissa nula e faz, com o mesmo, um ângulo de 45º (abertura para a direita).

2006, 1.ª Fase
EX2: Determine as projeções da reta i, de interseção dos planos oblíquos β e ω .
Dados:
– o plano β é definido pelas retas paralelas r e s;
– a reta r contém os pontos R (0; 1; 5) e S (1; 2; 3);
– a reta s contém o ponto T (4; 1; 2);
– os traços do plano ω intersetam-se num ponto com – 8 de abcissa: o traço horizontal faz um ângulo de 45º com o eixo x, e o traço frontal faz um ângulo de 60° com o mesmo eixo (ambos de abertura para a esquerda)

2002, 1.ª Fase, 1.ª Chamada
EX3: Determine a reta de interseção i dos dois planos ρ e θ .
Dados:
– o plano ρ é de rampa e é definido pelo seu traço frontal, que tem 3 de cota, e por uma reta a, fronto-horizontal, que tem 4 de afastamento e 1 de cota;
– o plano θ é de topo e faz um diedro de 30º (abertura para a direita, no primeiro diedro) com o plano horizontal de projeção.

AULA de HOJE - 09 de FEVEREIRO - 10ºB e 10ºA

10ºB e 10ºA - 8:15 às 10:05 e 15:20 às 17:10

Sumário: Exercícios de Interseções entre Planos

AULA de HOJE - 07 de FEVEREIRO - 11ºA

11ºA - 13:30 às 15:20

Sumário: CONTINUAÇÃO do ESTUDO DE SOMBRAS
- CONES REGULARES;

Exercícios de sombras de Cones Regulares.

vídeo aula - Cone com base horizontal

EXERCÍCIO:
Represente a sombra do mesmo cone do vídeo, mas invertendo a posição do vértice V que ficará com cota igual a 1 cm e a base com cota igual a 7 cm.

 10º A

Determine a reta i de intersecção entre um plano de rampa γ e
um plano de topo δ sabendo que:
 
·        O plano de rampa γ contém as retas fronto-horizontais a e b.
·        A recta a tem 3 cm de afastamento e 3cm de cota.
·        A recta b tem 5 cm de afastamento e 2cm de cota.
·        O plano de topo δ faz 45º (a.e.) com o P.H.P..

AULA de HOJE - 06 de FEVEREIRO - 10ºA e 10ºB

10ºA e 10ºB- 08:15 às 10:05 e 10:20 ás 12:10

 Sumário: Exercícios de consolidação das aprendizagens.

EXERCÍCIO 01 -  2008, 2.ª Fase (código 708) ADAPTADO
Represente pelas suas projeções uma pirâmide pentagonal oblíqua com base contida no plano horizontal de projeção, de acordo com os dados abaixo apresentados.
Dados:
– a base [ABCDE] é um pentágono regular inscrito na circunferência de centro O (4; 5; 0) e com 5 cm de raio;
– a face lateral [ABV] é frontal, (ou seja, está paralela ao Plano frontal de Projeção) e representa um triângulo isósceles sendo os seus vértices A e B os de menor afastamento da base;
– o vértice V da pirâmide tem 9 de cota;

EXERCÍCIO 02 - Determine as projeções de uma pirâmide quadrangular oblíqua

de 6,5 cm de altura, sabendo que:

Dados:
– o ponto O ( 0; 0; 6) é centro da base da pirâmide;
– o vértice V encontra-se numa abcissa de menos 5 cm em relação à abcissa
do ponto O, e pertence ao Plano Horizontal de projeção;

– o Ponto A ( 3; 0; 2) é um dos vértices da base.

EXERCÍCIO 03 - 2004, 2.ª Fase (código 409) 
Determine as projeções da reta horizontal h, contida num plano
Dados:
– o plano α é definido pelos pontos F (3; 0; 5), H (3; 2; 0) e P;
– o ponto P tem abcissa nula, 3 de cota e pertence ao bissetor dos diedros ímpares;
– a reta h interseta o plano frontal de projeção num ponto, Fh, com 2 de abcissa.

AULA de HOJE - 02 de FEVEREIRO - 11ºA

11ºA - 13:30 às 15:20

Sumário: CONTINUAÇÃO do ESTUDO DE SOMBRAS - SÓLIDOS REGULARES;

Exercícios de sombras de Prismas Regulares.

vídeo aula - Prisma hexagonal com bases frontais

ENUNCIADO do EXERCÍCIO PROF. JOÃO deste VÍDEO

- Determine as sombras próprias e projetadas de um prisma hexagonal regular com bases frontais e 4 cm de altura sabendo que:
- O Ponto O ( 0; 2; 4 ) é o centro da base de menor afastamento do prisma;

- O Ponto A ( 3; 2; 3 ) é um dos vértices dessa base;
- O foco de luz é o convencional.

EXERCÍCIO RETIRADO DO

SITE de Geometria da escola Infanta Dona Maria II de Braga

para realizar (e enviar por mail) até ao final desta aula.

Represente um cubo, situado no 1º diedro, de acordo com os dados abaixo apresentados.
Utilizando a direção luminosa convencional, determine a sombra própria do cubo e a sua sombra real projetada nos planos de projeção.
- a face [ABCD] do cubo é paralela ao plano frontal de projeção;
- os pontos A e B são dois vértices consecutivos da face [ABCD];
- o vértice A tem abcissa nula, 2 de afastamento e 5 de cota;
- o vértice B tem 4 de abcissa e 3 de cota.

BOM TRABALHO

JS

AULA de HOJE - 01 de FEVEREIRO - 10ºA

10ºA e 10ºB- 09:15 às 11:10

 Sumário: Correção da prova de avaliação.

Introdução ao estudo de circunferências em Planos verticais e/ou de Topo.

Item 1: Determine as projeções de um plano de rampa ψ sabendo que:

·      O plano de rampa contém uma reta oblíqua a;

·      A reta a contém o ponto A ( -2; 3; -6 ) e as suas projeções frontal e horizontal fazem, respetivamente, 30º (a.d) e 60º (a.d.) com o eixo X.

·      Determine, ainda, as projeções de um ponto B existente no plano de rampa ψ , sabendo que o ponto B tem abcissa de 4 cm e cota igual a - 2 cm;                                                       

 

 

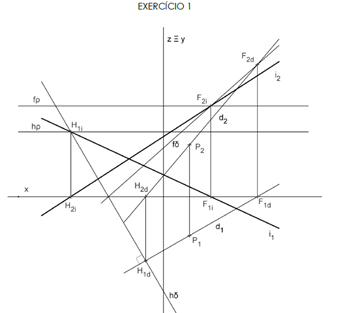
Item 2: Represente as projeções de duas retas a e b, concorrentes no ponto L ( 5; 5; 3 ).

·      A reta a tem as projeções paralelas entre si e a sua projeção horizontal faz 45º (a.d) com o eixo X.

·      A reta b é concorrente com o eixo X num ponto M, e a sua projeção horizontal é perpendicular à projeção horizontal da reta a.

·      Determine as projeções dos traços do plano definido pelas duas retas.               

 

 

Item 3: Determine as projeções de um plano oblíquo 𝞭 e de uma reta f frontal desse plano sabendo que:

·      O plano contém duas retas c e d, concorrentes no ponto Q ( 0; 0; 0 ).

·      A reta c contém o ponto C ( 2; -2; 2 ).

·      A reta d contém o ponto D ( 9; 3; 3 ).

·      A reta frontal f tem -4 cm de afastamento.                                                          

 

 

Item 4: Represente uma pirâmide hexagonal oblíqua, situada no primeiro diedro, sabendo que:

·      A base da pirâmide é o hexágono regular [ABCDEF], contido num plano horizontal;

·      A base está inscrita numa circunferência com centro no ponto O (0; 6; 9);

·      A vértice A da base da pirâmide tem - 4 cm de abcissa e 7 cm de afastamento;

·      A vértice V da pirâmide tem - 6 cm de abcissa e 3 cm de afastamento;

·      A aresta AV está contida numa reta oblíqua passante.

     

CÍRCULO EM; PLANO VERTICAL - Método do rebatimento

EXERCÍCIO círculo em plano vertical:
Determine as projeções de um círculo existente num plano vertical Teta sabendo que;
- O ponto O ( 0; 5; 3 ) é o centro do círculo que é tangente ao Plano Horizontal de Projeção;
- O plano vertical faz 60º (a.e.) com o eixo X.

EXERCÍCIO de HEXÁGONO em PLANO VERTICAL
Represente o hexágono regular [ABCDEF], situado no 1º diedro

contido num plano vertical ómega.
Dados:
- o ponto A (0; 3; 5) é um dos vértices do hexágono;
- a diagonal [AD] do hexágono esta contida numa recta obliqua d, cujas projecções, horizontal e frontal, fazem com o eixo x, ângulos respectivamente iguais a 60° (de abertura a esquerda) e 30° (de abertura a direita);
- os lados do hexágono medem 3 cm.

FIGURAS CONTIDAS EM PLANOS VERTICAIS

EXERCÍCIO – Exame Nacional de 2004, 2ª Fase (código 409)
Represente o quadrado [ABCD], situado no primeiro diedro.

Dados:
- o quadrado está contido num plano vertical Pi, cujo traço horizontal faz um ângulo de 45º
com o eixo x, de abertura para a direita;
- o quadrado está inscrito numa circunferência com centro no ponto O (0; 4; 6) e 3,5 cm de raio;
- o vértice A do quadrado tem -1 de abcissa;
- A é o vértice de maior cota.