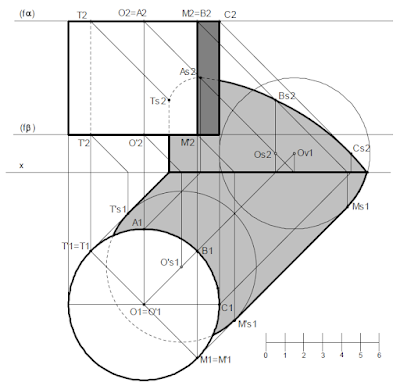
FIGURAS CONTIDAS EM PLANOS DE TOPO
EXERCÍCIO 01 - 1997, 2ª Fase (código 109)
Desenhe as projeções de um hexágono regular [ABCDEF], existente no primeiro diedro e contido num plano de topo β.
Dados:
- o plano de topo β faz um diedro de 45º, de abertura para a direita, com o plano horizontal de projeção;
- os pontos A (0; 4; 0) e B (0; 9; 0) são dois vértices consecutivos da figura.
EXERCÍCIO 02 – 2004, 2ª Fase (código 409)
Represente o quadrado [ABCD], situado no primeiro diedro.
Dados:
- o quadrado está contido num plano vertical 𝞭;, cujo traço horizontal faz um ângulo de 45º com o eixo x, de abertura para a direita;
- o quadrado está inscrito numa circunferência com centro no ponto O(0; 4; 6) e 3,5 cm de raio;
- o vértice A do quadrado tem -1 de abcissa;
- A é o vértice de maior cota.